6  Moderated mediation and mediated moderation

6.1 The simplest scenario: when \(X\) is continuous

6.1.1 Continuous Z

Now we are interested in a more complex model combining mediation and moderation. Specifically, we would like to know whether the mediation effect is different at different values of a moderator, that is, a moderated mediation model.

Likewise, we are investigating the relationship between \(X\) and \(Y\) and want to know the detailed mechanism of how \(X\) is affecting \(Y\).

In moderated mediation, the relationship between \(X\) and \(Y\) without mediator \(M\) (direct effect) can be moderated by moderator \(Z\) \[\begin{align*} Y&=c_0+c_1X+c_2Z+c_3XZ+\epsilon_Y. \end{align*}\]

6.1.1.1 Full moderated mediation model

Now assume that the relationship between \(X\) and \(Y\) is mediated by \(M\) while the mediation effect is moderated by \(Z\). More specifically, we assume:

1. the effect of \(X\) on \(M\) (path between \(X\) and \(M\)) is moderated by \(Z\);
2. the effect of \(M\) on \(Y\) (path between \(M\) and \(Y\)) is moderated by \(Z\);
3. the effect of \(X\) on \(Y\) (path between \(X\) and \(Y\)) is moderated by \(Z\).

Thus we have a full moderated mediation model, of which the path diagrams are

Figure 6.1: Full moderated mediation model

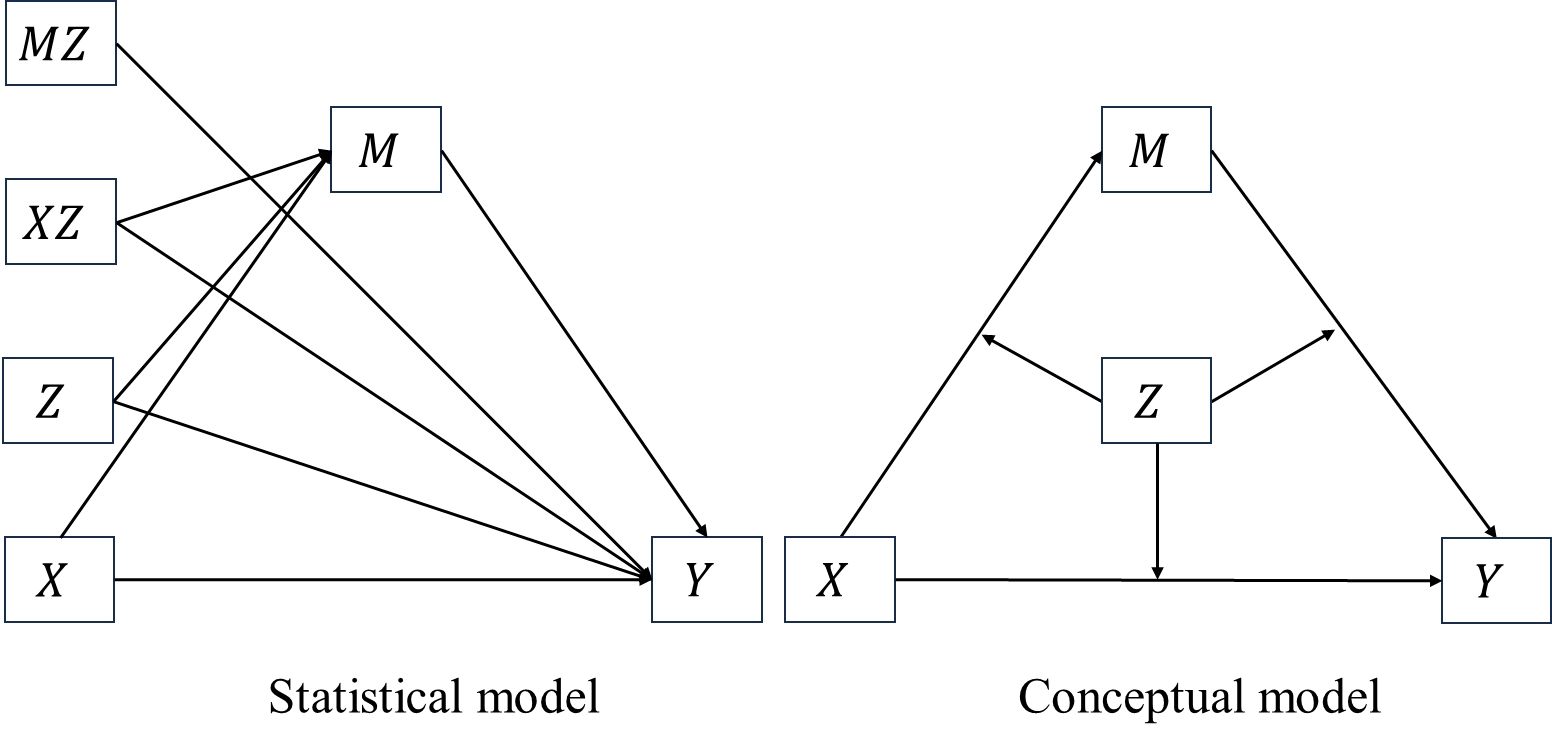
and the equations are \[\begin{align*} M&=a_0+a_1X+a_2Z+a_3XZ+\epsilon_M\\ Y&=c_0'+c_1'X+c_2'Z+c'_3XZ+b_1M+b_2MZ+\epsilon_Y. \end{align*}\] By combining the two equations above we have \[\begin{align*} Y&=c_0'+c_1'X+c_2'Z+c'_3XZ+\\ &\quad \enspace b_1(a_0+a_1X+a_2Z+a_3XZ+\epsilon_M)+\\ &\quad \enspace b_2(a_0+a_1X+a_2Z+a_3XZ+\epsilon_M)Z+\epsilon_Y\\ &=c_0'+c_2'Z+(c_1'+c_3'Z)X+\\ &\quad \enspace b_1(a_0+a_2Z)+b_1(a_1+a_3Z)X+b_1\epsilon_M+\\ &\quad \enspace b_2(a_0+a_2Z)Z+b_2Z(a_1+a_3Z)X+b_2Z\epsilon_M+\epsilon_Y\\ &= c_0'+c_2'Z+(a_0+a_2Z)(b_1+b_2Z)+\\ &\quad \enspace [\green(c_1'+c_3'Z)+\blue(a_1+a_3Z)\red(b_1+b_2Z)\black]X+ \\ &\quad \enspace \grey(b_1+ b_2Z)\epsilon_M+\epsilon_Y. \end{align*}\]

Figure 6.2: Full moderated mediation with labels

In this full moderated mediation model, the mediation effect is \((a_1+a_3Z)(b_1+b_2Z)\); the moderation effects of three moderated paths are

1. \(a_3\), the path between \(X\) and \(M\) is moderated by \(Z\);
2. \(b_2\), the path between \(M\) and \(Y\) is moderated by \(Z\);
3. \(c_3'\), the path between \(X\) and \(Y\) is moderated by \(Z\).

If we did not assume the path between \(X\) and \(Y\) is moderated by \(Z\), then we replace \(c_3'\) with 0 in above equations, the resulting conceptual model is

Figure 6.3: Full moderated mediation (direct effect not moderated) with labels

We can simplify the full moderated mediation model by assuming that only parts of the paths in the basic mediation model are moderated by \(Z\).

6.1.1.2 First stage moderated mediation model

In this model, we assume that

1. the path between \(X\) and \(M\) is moderated by \(Z\);
2. the path between \(X\) and \(Y\) is moderated by \(Z\).

Thus we have

Figure 6.4: First stage moderated mediation

and \[\begin{align*} M&=a_0+a_1X+a_2Z+a_3XZ+\epsilon_M\\ Y&=c_0'+c_1'X+c_2'Z+c'_3XZ+b_1M+\epsilon_Y. \end{align*}\] By combining these two equations \[\begin{align*} Y&=c_0'+c_1'X+c_2'Z+c'_3XZ+\\ &\quad \enspace b_1(a_0+a_1X+a_2Z+a_3XZ+\epsilon_M)+\epsilon_Y\\ &=c_0'+c_2'Z+(c_1'+c_3'Z)X+\\ &\quad \enspace b_1(a_0+a_2Z)+b_1(a_1+a_3Z)X+b_1\epsilon_M+\epsilon_Y\\ &= c_0'+c_2'Z+(a_0+a_2Z)b_1+\\ &\quad \enspace [\green(c_1'+c_3'Z)+\blue(a_1+a_3Z)\red b_1\black]X+ \\ &\quad \enspace \grey b_1\epsilon_M+\epsilon_Y. \end{align*}\] In this first stage moderated mediation model, the mediation effect is \((a_1+a_3Z)b_1\); the moderation effects of two moderated paths are

1. \(a_3\), the path between \(X\) and \(M\) is moderated by \(Z\);
2. \(c_3'\), the path between \(X\) and \(Y\) is moderated by \(Z\).

Figure 6.5: First stage moderated mediation with labels

If we did not assume the path between \(X\) and \(Y\) is moderated by \(Z\), then we replace \(c_3'\) with 0 in above equations, the resulting conceptual model is

Figure 6.6: First stage moderated mediation (direcr effect not moderated) with labels

6.1.1.3 Second stage moderated mediation model

In this model, we assume that

1. the path between \(M\) and \(Y\) is moderated by \(Z\);
2. the path between \(X\) and \(Y\) is moderated by \(Z\).

Thus we have

Figure 6.7: Second stage moderated mediation

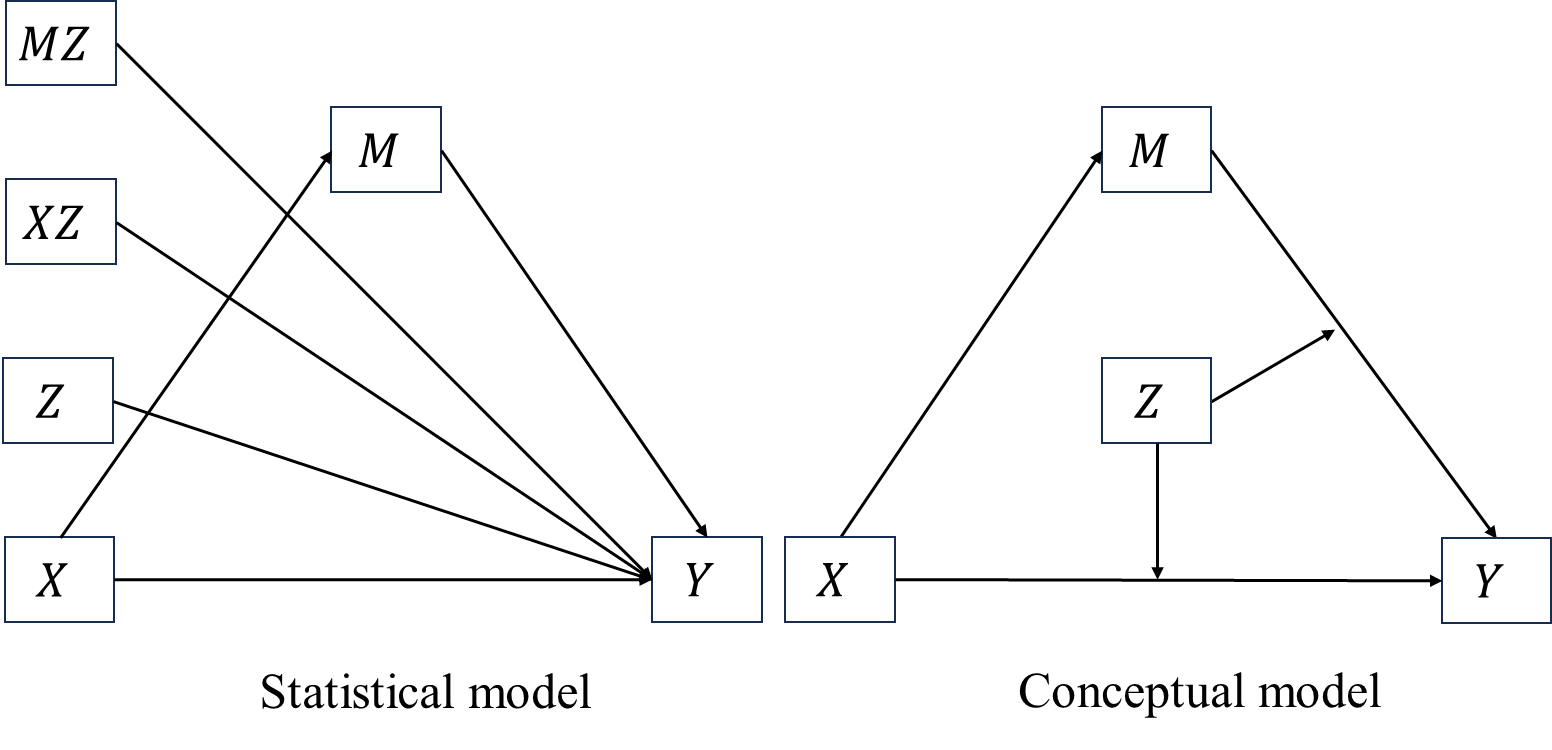
and \[\begin{align*} M&=a_0+a_1X+\epsilon_M\\ Y&=c_0'+c_1'X+c_2'Z+c'_3XZ+b_1M+b_2MZ+\epsilon_Y. \end{align*}\] By combining these two equations \[\begin{align*} Y&=c_0'+c_1'X+c_2'Z+c'_3XZ+\\ &\quad \enspace b_1(a_0+a_1X+\epsilon_M)+\\ &\quad \enspace b_2(a_0+a_1X+\epsilon_M)Z+\epsilon_Y\\ &=c_0'+c_2'Z+(c_1'+c_3'Z)X+\\ &\quad \enspace b_1a_0+b_1a_1X+b_1\epsilon_M+\\ &\quad \enspace b_2a_0Z+b_2a_1ZX+b_2Z\epsilon_M+\epsilon_Y\\ &= c_0'+c_2'Z+a_0(b_1+b_2Z)+\\ &\quad \enspace [\green(c_1'+c_3'Z)+\red a_1\blue(b_1+b_2Z)\black]X+ \\ &\quad \enspace \grey(b_1+ b_2Z)\epsilon_M+\epsilon_Y. \end{align*}\]

In second stage moderated mediation model, the mediation effect is \(a_1(b_1+b_2Z)\); the moderation effects of two moderated paths are

1. \(b_2\), the path between \(M\) and \(Y\) is moderated by \(Z\);
2. \(c_3'\), the path between \(X\) and \(Y\) is moderated by \(Z\).

Figure 6.8: Second stage moderated mediation with labels

If we did not assume the path between \(X\) and \(Y\) is moderated by \(Z\), then we replace \(c_3'\) with 0 in above equations, the resulting conceptual model is

Figure 6.9: Second stage moderated mediation (direct effect not moderated) with labels

6.1.1.4 Moderated mediation analysis

Because in a moderated mediation model, we are most interested in the mediation effect and want to know if it is moderated by \(Z\), thus the analysis consists of two steps:

1. moderation analysis,
2. simple mediation analysis.

These two steps are similar to what we have learned in basic moderation analysis, we first want to know the significance of hypothesized moderation effect (significance of interaction effect in ANOVA), if so, we then want to know how does the effect of \(X\) on \(Y\) is moderated by \(Z\) by conducting simple slope analysis (simple main effect analysis in ANOVA).

1. Significance test of moderation effect(s).

The effect of \(X\) on \(Y\) in full moderated mediation model is

\[\green(c_1+c_3'Z)+\blue(a_1+a_3Z)\red(b_1+b_2Z)\black,\] as long as at least one of \(c'\), \(a_3\) or \(b_2\) is non-zero, the effect of \(X\) on \(Y\) is moderated by \(Z\). But testing these 3 coefficients separately leads to floated type-I error rate and low power issue, so we test the products instead.

The equation above can be rewritten as \[c_1+a_1b_1+c_3'Z+a_1b_2Z+a_3b_1Z+a_3b_2Z^2,\] where the coefficients of the last 4 terms, \(c_3'\), \(a_1b_2\), \(a_3b_1\), and \(a_3b_2\), are the moderation effects, or moderated mediation parts. If any of these 4 coefficients is non-zero, the effect of \(X\) on \(Y\) is moderated by \(Z\). We use bootstrap method to test the significance of \(c_3'\), \(a_1b_2\), \(a_3b_1\), and \(a_3b_2\). More specifically,

• if \(a_1b_2\), \(a_3b_1\), and \(a_3b_2\) were all non-zero, we have full moderated mediation model with (\(c_3'\neq0\)) or without (\(c_3'=0\)) direct path being moderated,
• if \(a_3b_1\neq0\), we have first stage moderated mediation model with (\(c_3'\neq0\)) or without (\(c_3'=0\)) direct path being moderated,
• if \(a_1b_2\neq0\), we have second stage moderated mediation model with (\(c_3'\neq0\)) or without (\(c_3'=0\)) direct path being moderated.

2. Simple mediation analysis.

In basic moderation analysis, for categorical moderator, we just need to test the significance of \(K\) simple slopes, \(K\) is the level of \(Z\); for continuous moderator, we use either the pick-a-point method or the Johnson-Neyman method.

In moderated mediation analysis, we use exactly the same methods. In addition to the significance test of simple slope, we also need to test the significance of simple mediation effect (conditional indirect effect) calculated using simple slope.

6.1.2 Categorical \(Z\)

6.1.2.1 Full moderated mediation model

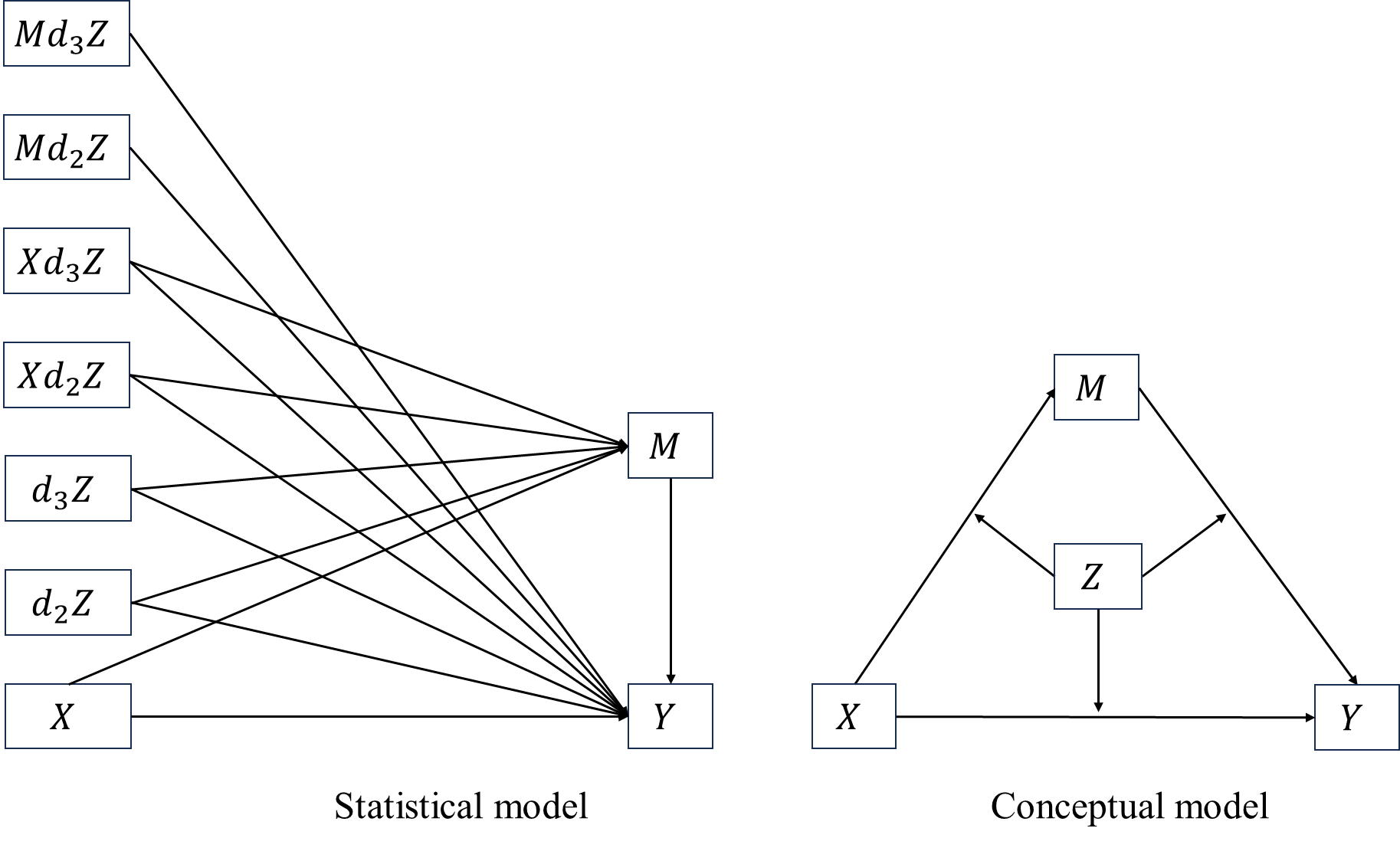
Suppose \(Z\) is a 3-level categorical variable and is dummy coded, the 1st category is used as the reference. The equations of a full moderated mediation model become \[\begin{align*} M&=a_0+a_1X+a_2d2Z+a_3d3Z+a_4Xd2Z+a_5Xd3Z+\epsilon_M\\ Y&=c_0'+c_1'X+c_2'd2Z+c'_3d3Z+c'_4Xd2Z+c'_5Xd3Z+\\ &\quad \enspace b_1M+b_2Md2Z+b_3Md3Z+\epsilon_Y. \end{align*}\] By combining the two equations above we have \[\begin{align*} Y&=c_0'+c_1'X+c_2'd2Z+c'_3d3Z+c'_4Xd2Z+c'_5Xd3Z+\\ &\quad \enspace b_1a_0+b_1a_1X+b_1a_2d2Z+b_1a_3d2Z+b_1a_4Xd2Z+b_1a_5Xd3Z+b_1\epsilon_M+\\ &\quad \enspace b_2a_0d2Z+b_2a_1Xd2Z+b_2a_2d2Zd2Z+b_2a_3d3Zd2Z+b_2a_4Xd2Zd2Z+\\ &\quad \enspace b_2a_5Xd3Zd2Z+b_2\epsilon_Md2Z+\\ &\quad \enspace b_3a_0d3Z+b_3a_1Xd3Z+b_3a_2d2Zd3Z+b_3a_3d3Zd3Z+b_3a_4Xd2Zd3Z+\\ &\quad \enspace b_3a_5Xd3Zd3Z+b_3\epsilon_M d3Z+\\ &\quad \enspace \epsilon_Y\\ &= c_0'+\\ &\quad \enspace (a_0+a_2d2Z+a_3d2Z)b_1+\\ &\quad \enspace (a_0+a_2d2Z+a_3d3Z)b_2d2Z+\\ &\quad \enspace (a_0+a_2d2Z+a_3d3Z)b_3d3Z+\\ &\quad \enspace c_2'd2Z+c'_3d3Z+\\ &\quad \enspace [\green(c_1'+c'_4d2Z+c'_5d3Z)+\\ &\quad \enspace \blue(a_1+a_4d2Z+a_5d3Z)\red b_1+\\ &\quad \enspace \blue(a_1+a_4d2Z+a_5d3Z)\red b_2d2Z+\\ &\quad \enspace \blue(a_1+a_4d2Z+a_5d3Z)\red b_3d3Z\black]X+\\ &\quad \enspace \grey(b_1+b_2d2Z+b_3d3Z)\epsilon_M+\epsilon_Y\\ &= c_0'+c_2'd2Z+c'_3d3Z+(a_0+a_2d2Z+a_3d2Z)(b_1+b_2d2Z+b_3d3Z)+\\ &\quad \enspace [\green(c_1'+c'_4d2Z+c'_5d3Z)+\blue(a_1+a_4d2Z+a_5d3Z)\red(b_1+b_2d2Z+b_3d3Z)\black] X+\\ &\quad \enspace \grey(b_1+b_2d2Z+b_3d3Z)\epsilon_M+\epsilon_Y. \end{align*}\]

It is obvious that we now have 3 simple mediations to test.

When \(Z=1\), \(d2Z=d3Z=0\), we have \[\begin{align*} Y|_{Z=1}&= c_0'+a_0b_1+\black(\green c_1'+\blue a_1\red b_1\black)X+\grey b_1\epsilon_M+\epsilon_Y \end{align*}\] When \(Z=2\), \(d2Z=1\),\(d3Z=0\), we have \[\begin{align*} Y&_{Z=2}= c_0'+(a_0+a_2)(b_1+b_2)+c_2'd2Z+\\ &\quad \enspace [\green(c_1'+c_4')+\blue(a_1+a_4)\red(b_1+b_2)\black]X+\\ &\quad \enspace \grey (b_1+b_2)\epsilon_M+\epsilon_Y. \end{align*}\] When \(Z=3\), \(d2Z=0\),\(d3Z=1\), we have \[\begin{align*} Y&_{Z=3}= c_0'+(a_0+a_3)(b_1+b_3)+c_3'd3Z+\\ &\quad \enspace [\green(c_1'+c_5')+\blue(a_1+a_5)\red(b_1+b_3)\black]X+\\ &\quad \enspace \grey (b_1+b_3)\epsilon_M+\epsilon_Y. \end{align*}\]

Figure 6.10: Full moderated mediation model (categorical Z)

Figure 6.11: Decomposition of X’s effect on Y when Z is categorical

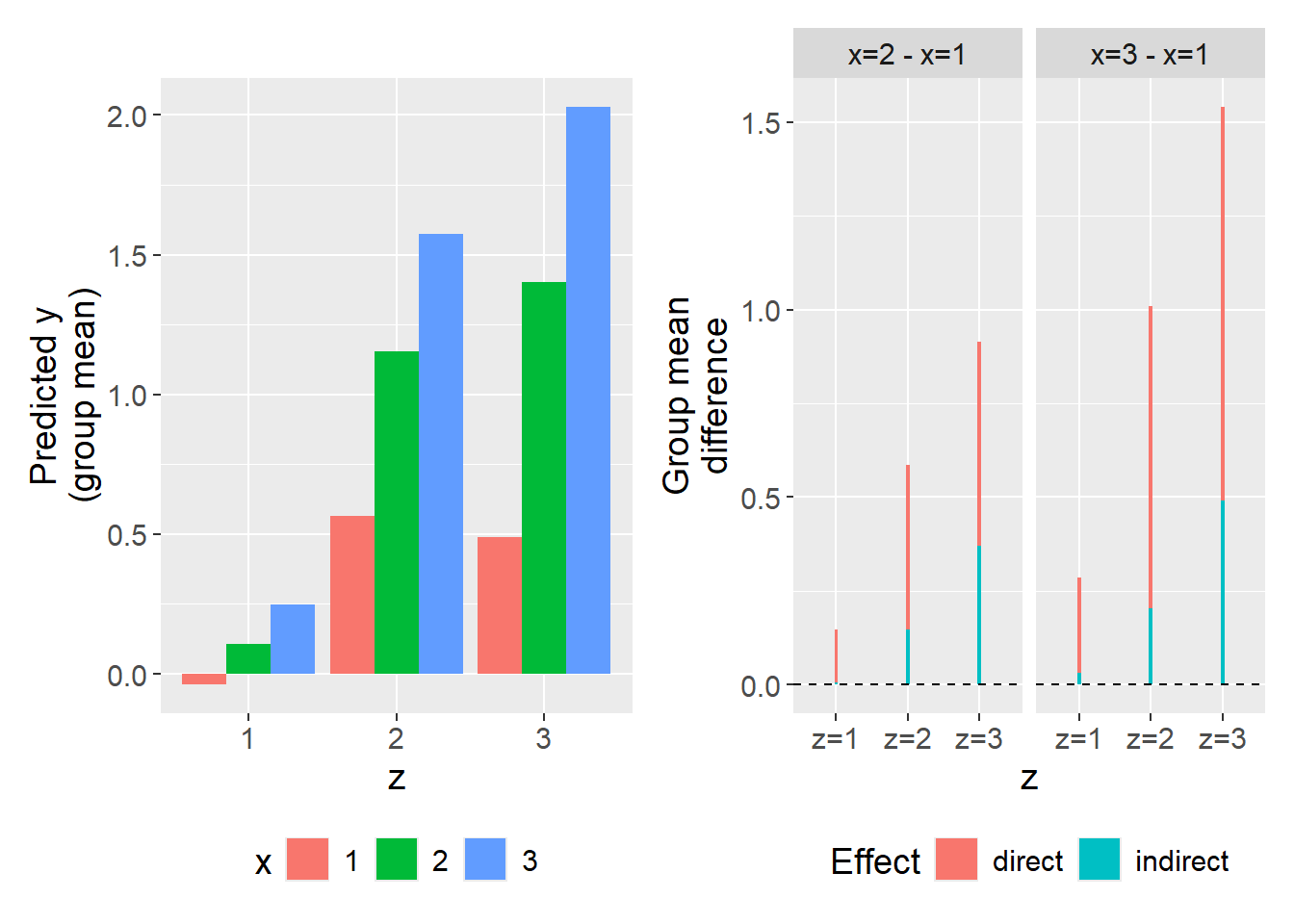
6.2 When \(X\) is categorical

6.2.1 Continuous \(Z\)

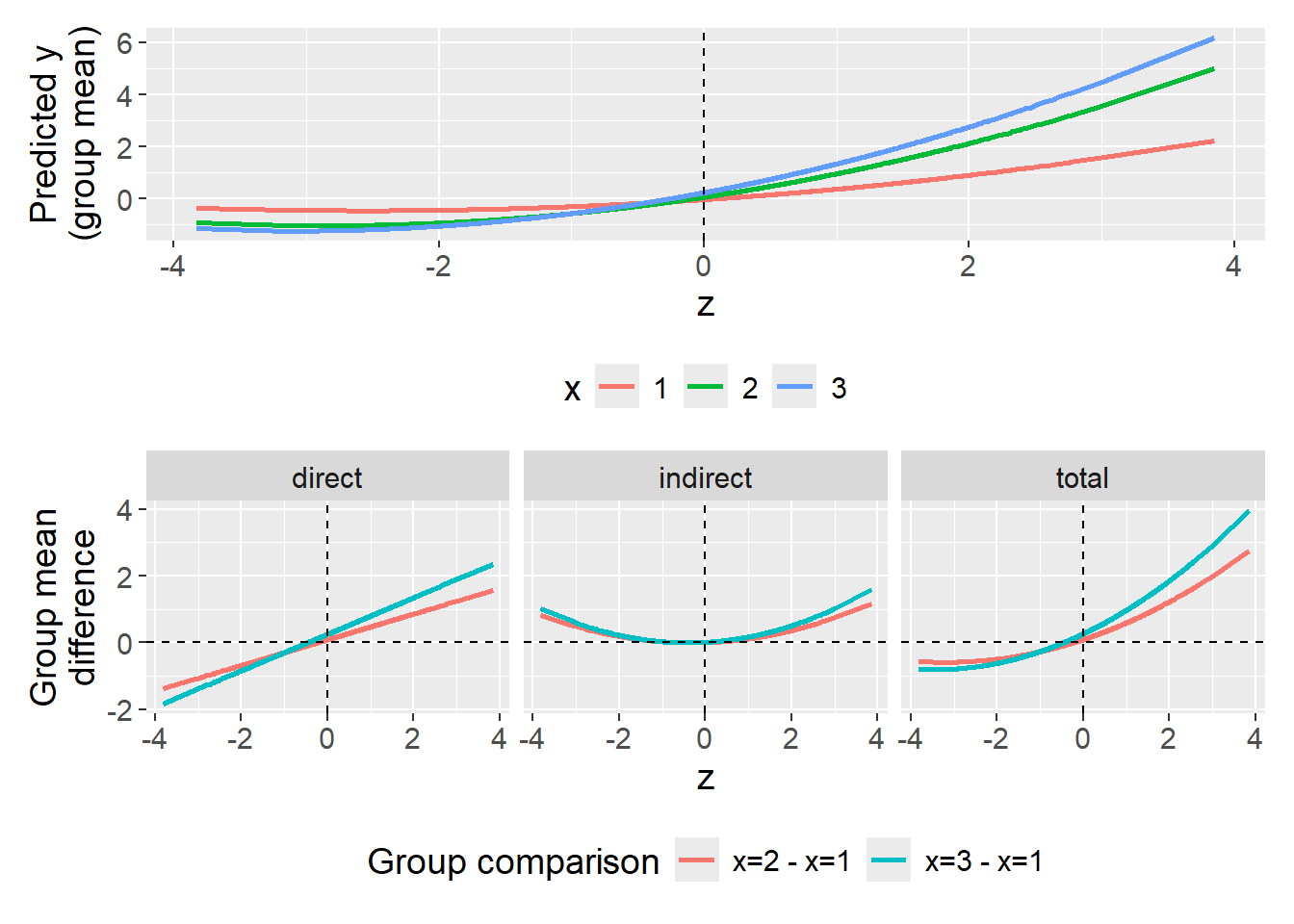
Suppose \(X\) is a 3-level categorical variable, of which the 1st category is used as reference group when dummy coding. The equations of a full moderated mediation model become \[\begin{align} M&=a_0+a_1d2X+a_2d3X+a_3Z+a_4d2XZ+a_5d3XZ+\epsilon_M\\ Y&=c_0'+c_1'd2X+c_2'd3X+c_3'Z+c_4'd2XZ+c_5'd3XZ+\\ &\quad \enspace b_1M+b_2MZ+\epsilon_Y. \end{align}\] By combining the two equations above we have \[\begin{align} Y&=c_0'+c_1'd2X+c_2'd3X+c_3'Z+c_4'd2XZ+c_5'd3XZ+\\ &\quad \enspace b_1a_0+b_1a_1d2X+b_1a_2d3X+b_1a_3Z+b_1a_4d2XZ+b_1a_5d3XZ+\\ &\quad \enspace b_2a_0Z+b_2a_1d2XZ+b_2a_2d3XZ+b_2a_3ZZ+b_2a_4d2XZZ+b_2a_5d3XZZ+\\ &\quad \enspace b_1\epsilon_M+b_2\epsilon_MZ+\epsilon_Y\\ Y&=c_0'+c_3'Z+b_1(a_0+a_3Z)+b_2Z(a_0+a_3Z)+\\ &\quad \enspace [c_1'+c_4'Z+b_1(a_1+a_4Z)+b_2z(a_1+a_4Z)]d2X+\\ &\quad \enspace [c_2'+c_5'Z+b_1(a_2+a_5Z)+b_2z(a_2+a_5Z)]d3X+\\ &\quad \enspace b_1\epsilon_M+b_2\epsilon_MZ+\epsilon_Y\\ Y&=(c_0'+c_3'Z)+(a_0+a_3Z)(b_1+b_2Z)+\\ &\quad \enspace [\green(c_1'+c_4'Z)+\blue(a_1+a_4Z)\red(b_1+b_2Z)\black]d2X+\\ &\quad \enspace [\green(c_2'+c_5'Z)+\blue(a_2+a_5Z)\red(b_1+b_2Z)\black]d3X+\\ &\quad \enspace \grey b_1\epsilon_M+b_2\epsilon_MZ+\epsilon_Y. \end{align}\]

When \(X=1\), \(d2X=d3X=0\), we have \[\begin{align} Y|_{X=1}&= (c_0'+c_3'Z)+(a_0+a_3Z)(b_1+b_2Z)+\\ &\quad \enspace \grey b_1\epsilon_M+b_2\epsilon_MZ+\epsilon_Y. \end{align}\]

When \(X=2\), \(d2X=1\),\(d3X=0\), we have \[\begin{align} Y&_{X=2}= (c_0'+c_3'Z)+(a_0+a_3Z)(b_1+b_2Z)+\\ &\quad \enspace \green(c_1'+c_4'Z)+\blue(a_1+a_4Z)\red(b_1+b_2Z)\black+\\ &\quad \enspace \grey b_1\epsilon_M+b_2\epsilon_MZ+\epsilon_Y. \end{align}\]

When \(X=3\), \(d2X=0\),\(d3X=1\), we have \[\begin{align} Y&_{X=3}= (c_0'+c_3'Z)+(a_0+a_3Z)(b_1+b_2Z)+\\ &\quad \enspace \green(c_2'+c_5'Z)+\blue(a_2+a_5Z)\red(b_1+b_2Z)\black+\\ &\quad \enspace \grey b_1\epsilon_M+b_2\epsilon_MZ+\epsilon_Y. \end{align}\]

Figure 6.12: Decomposition of X’s effect on Y when X is categorical and Z is continuous

6.2.2 Categorical \(Z\)

Suppose both \(X\) and \(Z\) are 3-level categorical variables. The 1st categories of \(X\) and \(Z\) are used as reference ones when dummy coding. The equations of a full moderated mediation model become \[\begin{align*} M&=a_0+a_1d2X+a_2d3X+a_3d2Z+a_4d3Z+\\ &\quad \enspace a_5d2Xd2Z+a_6d2Xd3Z+a_7d3Xd2Z+a_8d3Xd3Z+\epsilon_M\\ Y&=c_0'+c_1'd2X+c_2'd3X+c_3'd2Z+c_4'd3Z+\\ &\quad \enspace c_5'd2Xd2Z+c_6'd2Xd3Z+c_7'd3Xd2Z+c_8'd3Xd3Z+\\ &\quad \enspace b_1M+b_2Md2Z+b_3Md3Z+\epsilon_Y. \end{align*}\] By combining the two equations above we have \[\begin{align*} Y&=c_0'+c_1'd2X+c_2'd3X+c_3'd2Z+c_4'd3Z+\\ &\quad \enspace c_5'd2Xd2Z+c_6'd2Xd3Z+c_7'd3Xd2Z+c_8'd3Xd3Z+\\ &\quad \enspace b_1a_0+b_1a_1d2X+b_1a_2d3X+b_1a_3d2Z+b_1a_4d3Z+\\ &\quad \enspace b_1a_5d2Xd2Z+b_1a_6d2Xd3Z+b_1a_7d3Xd2Z+b_1a_8d3Xd3Z+\\ &\quad \enspace b_2a_0d2Z+b_2a_1d2Xd2Z+b_2a_2d3Xd2Z+b_2a_3d2Zd2Z+b_2a_4d3Zd2Z+\\ &\quad \enspace b_2a_5d2Xd2Zd2Z+b_2a_6d2Xd3Zd2Z+b_2a_7d3Xd2Zd2Z+b_2a_8d3Xd3Zd2Z+\\ &\quad \enspace b_3a_0d3Z+b_3a_1d2Xd3Z+b_3a_2d3Xd3Z+b_3a_3d2Zd3Z+b_3a_4d3Zd3Z+\\ &\quad \enspace b_3a_5d2Xd2Zd3Z+b_3a_6d2Xd3Zd3Z+b_3a_7d3Xd2Zd3Z+b_3a_8d3Xd3Zd3Z+\\ &\quad \enspace b_1\epsilon_M+b_2\epsilon_Md2Z+b_3\epsilon_Md3Z+\epsilon_Y\\ &=c_0'+c_3'd2Z+c_4'd3Z+\\ &\quad \enspace b_1(a_0+a_3d2Z+a_4d3Z)+b_2(a_0+a_3d2Z+a_4d3Z)d2Z+\\ &\quad \enspace \quad \quad (a_0+b_3a_3d2Z+b_3a_4d3Z)d3Z+\\ &\quad \enspace [(c_1'+c_5'd2Z+c_6'd3Z)+\\ &\quad \enspace (a_1+a_5d2Z+a_6d3Z)b_1+(a_1+a_5d2Z+a_6d3Z)b_2d2Z+\\ &\quad \enspace \quad \quad (a_1+a_5d2Z+a_6d3Z)b_3d3Z]d2X+\\ &\quad \enspace [(c_2'+c_7'd2Z+c_8'd3Z)+\\ &\quad \enspace (a_2+a_7d2Z+a_8d3Z)b_1+(a_2+a_7d2Z+a_8d3Z)b_2d2Z+\\ &\quad \enspace \quad \quad (a_2+a_7d2Z+a_8d3Z)b_3d3Z]d3X+\\ &\quad \enspace b_1\epsilon_M+b_2\epsilon_Md2Z+b_3\epsilon_Md3Z+\epsilon_Y\\ &=(c_0'+c_3'd2Z+c_4'd3Z)+(a_0+a_3d2Z+a_4d3Z)(b_1+b_2d2Z+b_3d3Z)+\\ &\quad \enspace [\green(c_1'+c_5'd2Z+c_6'd3Z)+\blue(a_1+a_5d2Z+a_6d3Z)\red(b_1+b_2d2Z+b_3d3Z)\black]d2X+\\ &\quad \enspace [\green(c_2'+c_7'd2Z+c_8'd3Z)+\blue(a_2+a_7d2Z+a_8d3Z)\red(b_1+b_2d2Z+b_3d3Z)\black]d3X+\\ &\quad \enspace \grey b_1\epsilon_M+b_2\epsilon_Md2Z+b_3\epsilon_Md3Z+\epsilon_Y. \end{align*}\]

Note

Note that, in the following equations, only the parts that differ from those in the reference group are shown in color.

\(Z=1\)

When \(X=1\) and \(Z=1\) (reference group), \(d2X=d3X=d2Z=d3Z=0\), we have \[\begin{align*} Y|_{X=1,Z=1}&= c_0'+ a_0b_1+\grey b_1\epsilon_M+\epsilon_Y. \end{align*}\]

When \(X=2\) and \(Z=1\), \(d2X=1\), \(d3X=d2Z=d3Z=0\), we have \[\begin{align*} Y|_{X=2,Z=1}&=c_0'+a_0b_1+\green c_1'+\blue a_1\red b_1\grey+ b_1\epsilon_M+\epsilon_Y. \end{align*}\]

When \(X=3\) and \(Z=1\), \(d3X=1\), \(d2X=d2Z=d3Z=0\), we have \[\begin{align*} Y|_{X=3,Z=1}&=c_0'+a_0b_1+\green c_2'+\blue a_2\red b_1\grey+b_1\epsilon_M+\epsilon_Y. \end{align*}\]

\(Z=2\)

When \(X=1\) and \(Z=2\), \(d2X=d3X=d3Z=0\), \(d2Z=1\), we have \[\begin{align*} Y|_{X=1,Z=2}&=(c_0'+c_3')+(a_0+a_3)(b_1+b_2)+\\ &\quad \enspace \grey b_1\epsilon_M+b_2\epsilon_M+\epsilon_Y\\ &=c_0'+a_0b_1+\green c_3'+\blue a_0\red b_2+\blue a_3\red b_1+\blue a_3\red b_2\grey+\\ &\quad \enspace \grey b_1\epsilon_M+b_2\epsilon_M+\epsilon_Y \end{align*}\]

When \(X=2\) and \(Z=2\), \(d2X=d2Z=1\), \(d3X=d3Z=0\), we have \[\begin{align*} Y|_{X=2,Z=2}&=(c_0'+c_3')+(a_0+a_3)(b_1+b_2)+\green(c_1'+c_5')+\blue(a_1+a_5)\red(b_1+b_2)\grey+\\ &\quad \enspace \grey b_1\epsilon_M+b_2\epsilon_M+\epsilon_Y\\ &=c_0'+a_0b_1+\green c_3'+\blue a_0\red b_2+\blue a_3\red b_1+\blue a_3\red b_2+\\ &\quad \enspace \green c_1'+c_5'+\blue a_1\red b_1+\blue a_1\red b_2+\blue a_5\red b_1+\blue a_5\red b_2\grey+\\ &\quad \enspace \grey b_1\epsilon_M+b_2\epsilon_M+\epsilon_Y. \end{align*}\]

When \(X=3\) and \(Z=2\), \(d3X=d2Z=1\), \(d2X=d3Z=0\), we have \[\begin{align*} Y|_{X=3,Z=2}&=(c_0'+c_3')+(a_0+a_3)(b_1+b_2)+\green(c_2'+c_7')+\blue(a_2+a_7)\red(b_1+b_2)+\\ &\quad \enspace \grey b_1\epsilon_M+b_2\epsilon_M+\epsilon_Y\\ &=c_0'+a_0b_1+\green c_3'+\blue a_0\red b_2+\blue a_3\red b_1+\blue a_3\red b_2+\\ &\quad \enspace \green c_2'+c_7'+\blue a_2\red b_1+\blue a_2\red b_2+\blue a_7\red b_1+\blue a_7\red b_2\grey+\\ &\quad \enspace \grey b_1\epsilon_M+b_2\epsilon_M+\epsilon_Y. \end{align*}\]

\(Z=3\)

When \(X=1\) and \(Z=3\), \(d2X=d3X=d2Z=0\), \(d3Z=1\), we have \[\begin{align*} Y|_{X=1,Z=3}&=(c_0'+c_4')+(a_0+a_4)(b_1+b_3)+\\ &\quad \enspace \grey b_1\epsilon_M+b_3\epsilon_M+\epsilon_Y\\ &=c_0'+a_0b_1+\green c_4'+\blue a_0\red b_3+\blue a_4\red b_1+\blue a_4\red b_3\grey+\\ &\quad \enspace \grey b_1\epsilon_M+b_3\epsilon_M+\epsilon_Y. \end{align*}\]

When \(X=2\) and \(Z=3\), \(d2X=d3Z=1\), \(d3X=d2Z=0\), we have \[\begin{align*} Y|_{X=2,Z=3}&=(c_0'+c_4')+(a_0+a_4)(b_1+b_3)+\green(c_1'+c_6')+\blue(a_1+a_6)\red(b_1+b_3)+\\ &\quad \enspace \grey b_1\epsilon_M+b_3\epsilon_M+\epsilon_Y\\ &=c_0'+a_0b_1+\green c_4'+\blue a_0\red b_3+\blue a_4\red b_1+\blue a_4\red b_3+\\ &\quad \enspace \green c_1'+c_6'+\blue a_1\red b_1+\blue a_1\red b_3+\blue a_6\red b_1+\blue a_6\red b_3\grey+\\ &\quad \enspace \grey b_1\epsilon_M+b_3\epsilon_M+\epsilon_Y. \end{align*}\]

When \(X=3\) and \(Z=3\), \(d3X=d3Z=1\), \(d2X=d2Z=0\), we have \[\begin{align*} Y|_{X=3,Z=3}&=(c_0'+c_4')+(a_0+a_4)(b_1+b_3)+\green(c_2'+c_8')+\blue(a_2+a_8)\red(b_1+b_3)+\\ &\quad \enspace \grey b_1\epsilon_M+b_3\epsilon_M+\epsilon_Y\\ &=c_0'+a_0b_1+\green c_4'+\blue a_0\red b_3+\blue a_4\red b_1+\blue a_4\red b_3+\\ &\quad \enspace \green c_2'+c_8'+\blue a_2\red b_1+\blue a_2\red b_3+\blue a_8\red b_1+\blue a_8\red b_3\grey+\\ &\quad \enspace \grey b_1\epsilon_M+b_3\epsilon_M+\epsilon_Y. \end{align*}\]

Figure 6.13: Decomposition of X’s effect on Y when both X and Z are categorical

6.3 How to report moderated mediation analysis

8.3 section in Ye et al. (2024)

6.4 Real data example

In the following section, we use a real data example from EPSY:579 R cookbook for SEM by Ge Jiang.

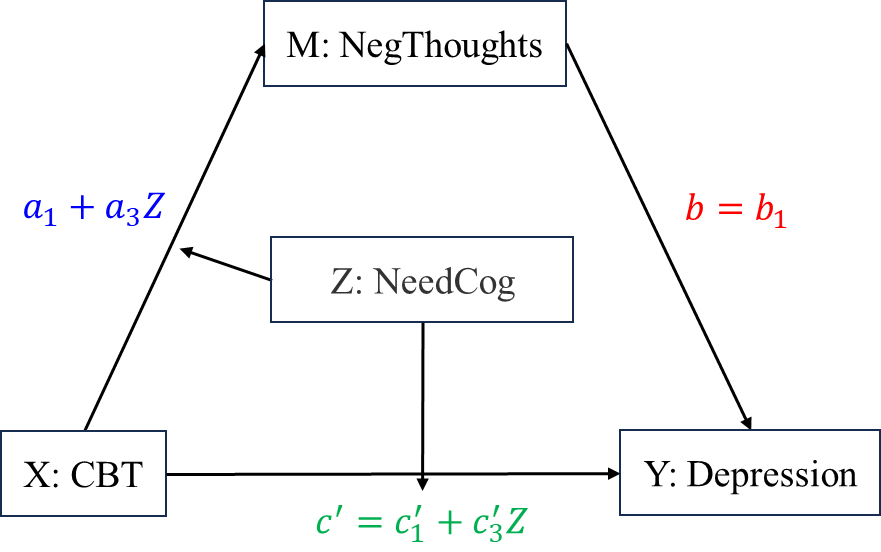
In this example, we fit the first stage moderated mediation model without moderated direct path, that is, we assume that the path between CBT and NegThoughts is moderated by NeedCog. Therefore, the moderation effect to-test is \(a3b1\).

6.4.1 Categorical \(Z\)

• X: CBTDummy, cognitive behavioral therapy
• M: NegThoughts, negative thoughts
• Y: Depression
• Z: NeedCog, need for cognition, a psychological construct that refers to an individual’s desire for, and enjoyment of, intellectually engaging activities. As such, a substantial amount of research has shed light on how need for cognition is associated with numerous positive outcomes, such as learning and academic success, and also how it is associated to theoretically related constructs found in the literature (e.g., intellectual engagement, epistemic curiosity).

Interpretation: needCog significantly moderates CBT -> NegThoughts -> Depression indirect effect through moderating the first stage of the indirect effect. Since we expect the effect of CBT on Depression to be negative (CBT reduces Depression). And IndexOfModMed \(a_3b_1\) is also negative. We’ll say NeedCog strengthens the indirect effect of CBT on Depression through NegThoughts. The higher need for cognition, the stronger the indirect effect, and the more effect mediated by NegThoughts.

6.4.2 Continuous \(Z\)

Now, we use the continuous version of NeedCog, NeedCogCont.

• Pick-a-point (recommended)

Interpretation is similar to the one of categorical moderator.

• Johnson-Neyman

The Johnson-Neyman for the output of SEM() has not being implemented yet.

6.5 Mediated moderation

Mediated moderation and moderated mediation are the two sides of one coin (Muller et al., 2005).

6.5.1 How to report mediated moderation

Section 5.1.3 in Liu and Wang (2024)

Muller, D., Judd, C. M., & Yzerbyt, V. Y. (2005). When moderation is mediated and mediation is moderated. Journal of Personality and Social Psychology, 89(6), 852.

Ye, W., Xu, S., & Zhou, X. (2024). Impact of repeated two-syllable brand names on consumer ethical responses in different moral contexts: A mind perception theory perspective. Acta Psychologica Sinica, 56(5), 650–669. https://doi.org/10.3724/SP.J.1041.2024.00650